Elliptikus görbén alapuló titkosírás
Csirmaz László, CEU
A nyilvános kulcsú titkosírás hátterében egy-egy matematikai probléma áll, melyrõl azt tételezzük fel, hogy nehéz megoldani. A Ron L. Rivest, Adi Shamir és Leon Adleman nevéhez fûzõdõ RSA módszer azt használja, hogy míg viszonylag egyszerû eldönteni, hogy egy több száz jegyû szám összetett-e vagy sem, addig prímtényezõire bontani már reménytelenül nehéz feladat. Whitheld Diffie és M. E. Hellmann nevét viselõ módszer hátterében az úgynevezett diszkrét logaritmus probléma áll: adott az alap és a hatványozás eredménye, keressük meg a kitevõt. A hatványozás természetesen ismételt szorzás, viszont a szorzást nem a szokásos, általános iskolában tanult módon kell elvégezni, hanem maradékosan, valamilyen elõre meghatározott prímszám modulussal. A problémát általánosan is meg lehet fogalmazni, a következõképpen: definiáljunk egy szorzásnak nevezett mûveletet sok (tipikusan 10100) elem között. Választunk egy g alapot, egy n kitevõt, és kiszámítjuk a y=gn hatványt. A feladat y és g ismeretében megkeresni az n kitevõt. Mivel az n kitevõ is 100 jegyû szám, az y hatvány kiszámítása sem lehetséges ismételt szorzással. Ezért még feltesszük, hogy a definiált mûvelet az adott elemeken csoportot alkot. Ilyenkor a hatványozást jóval gyorsabban el tudjuk végezni: a g generátor elemet ismételten négyzetre emeljük (ehhez egy-egy szorzást használva), amivel megkapjuk g-nek a 20, 21, 22, 23, stb kitevõs hatványait. Az n kitevõt kettes számrendszerben írjuk fel, és a jegyeinek megfelelõ hatványokat szorozzuk össze. Ezzel a szorzások számát még száz jegyû kitevõ esetén is 1000 alatt tudjuk tartani.
Diszkrét Logaritmus probléma
Adott egy G csoportban a g generáló valamint egy y elem. Keressük meg az y rendjét, vagyis azt n kitevõt, amire a csoportban gn=y.
Diffie és Hellmann ismerték fel, hogy véges csoportokon a diszkrét logaritmus nehéz probléma, vagyis a kitevõt az alap és a hatvány értékébõl nem lehet gyorsan visszakeresni. (Természetesen nem ez a helyzet a valós számok esetében, ekkor a kitevõt – vagyis y-nak g alapú logaritmusát – gyorsan ki tudjuk számítani.) Különbözõ speciális csoportok esetén más és más, igen bonyolult és mély matematikai eszközöket használó algoritmusokat fejlesztettek ki. Tetszõleges csoportra mûködõ leggyorsabb ismert algoritmus futásideje a csoport elemszámának négyzetgyökével arányos. Vagyis 10100 elemû csoportnál az algoritmus futása 1050 körüli mûveletet igényel, amit összevetve a világegyetem korára becsült becsült 1022 évvel, elég meggyõzõ érv a probléma nehézségére. Speciális csoportokon – így például egy p prímszámmal való maradékos szorzás esetén is – gyorsabb algoritmusok is ismeretesek. Abban az esetben, mikor a csoport éppen a modulo p összeadás, g pedig az 1 szám, igazán nincs is feladat, hiszen az eredmény és a kitevõ (jelen esetben a szorzótényezõ, hiszen most a mûvelet összeadás) egy és ugyanaz. Ez is mutatja, hogy kriptorendszer biztonsága szempontjából igen fontos a felhasznált csoport megfelelõ megválasztása.
Kriptográfiai
rendszerekben két típusú csoportot szokás
használni. Az egyik a az 1, 2, ¼,
p-1 számokon a modulo p maradékos szorzás
alkotta csoport. Ezekre a csoportokra ismeretes a fent említett
![]() idejû
általános algoritmusnál gyorsabb eljárás
is. Ha a p prímszám ezen kívül
még speciális alakú is, például
p-1-nek (vagy p+1-nek)
mindegyik prímosztója legfeljebb 10 jegyû, akkor
a diszkrét logaritmus problémát emberi idõ
alatt (néhány hónap vagy év) is meg lehet
oldani. A csoportoknak egy másik gazdag, és
egyre többet használt forrása az elliptikus
görbék.
Általános elliptikus görbékbõl adódó
csoportok esetén a diszkrét logaritmus problémára
nem ismeretes a csoport méretének gyökénél
kevesebb mûveletet igénylõ algoritmus.
Természetesen vannak kifejezetten rossz, illetve “nem
ajánlott” görbék, viszont elliptikus
görbékbõl jóval több van, mint
természetes számokból, nagyobb a választási
lehetõség, kisebb esélyünk van arra, hogy
egy rossz csoportba botlunk.
idejû
általános algoritmusnál gyorsabb eljárás
is. Ha a p prímszám ezen kívül
még speciális alakú is, például
p-1-nek (vagy p+1-nek)
mindegyik prímosztója legfeljebb 10 jegyû, akkor
a diszkrét logaritmus problémát emberi idõ
alatt (néhány hónap vagy év) is meg lehet
oldani. A csoportoknak egy másik gazdag, és
egyre többet használt forrása az elliptikus
görbék.
Általános elliptikus görbékbõl adódó
csoportok esetén a diszkrét logaritmus problémára
nem ismeretes a csoport méretének gyökénél
kevesebb mûveletet igénylõ algoritmus.
Természetesen vannak kifejezetten rossz, illetve “nem
ajánlott” görbék, viszont elliptikus
görbékbõl jóval több van, mint
természetes számokból, nagyobb a választási
lehetõség, kisebb esélyünk van arra, hogy
egy rossz csoportba botlunk.
Az elliptikus görbék a középiskolából jól ismert kör, ellipszis, parabola, hiperbola általánosításai. Míg például az egységkör a síknak azokból az (x,y) koordinátájú pontjaiból áll, amikre x2+y2=1, addig például az y2=x3+ax+b egyenletet kielégítõ pontok egy harmadrendû algebrai görbét határoznak meg.



y2=x3+ax+b egyenletû elliptikus görbék különbözõ paraméterekkel
Az ábrán különbözõ a és b paraméterek mellett mutatjuk be magát a görbét. A görbe maga egy vagy két részbõl áll, a jobb oldali ágai egyre meredekebben tartanak a végtelenbe. Azokat, melyek elmetszik saját magukat, vagy csúcsban végzõdnek, mint az a=b=0 esetben, szinguláris görbéknek nevezzük. A függõleges egyeneseket kivéve minden más egyenes vagy egy vagy három pontban metszi a görbét, ezért a függõleges egyenesek ideális (végtelen távoli) pontját is hozzá szokás venni a görbéhez, hogy azok se legyenek kivételek. A görbének ezt a pontját egy projektív transzformációval az origóba vive a görbe formája is megváltozik:
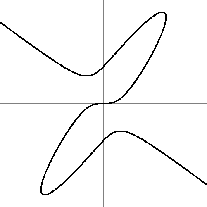

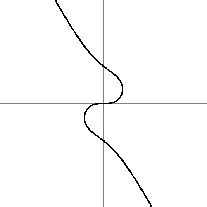
x3=y+axy2+by3 egyenletû duális görbék, az inflexiós pont az origó
Egyetlen olyan pont van, ahol az érintõ harmadrendben simul a görbéhez, ezt a görbe inflexiós pontjának nevezzük. Az y2=x3+ax+b egyenletû görbéknél ez a függõleges egyenesek ideális pontja, az x3=y+axy2+by3 görbéknél viszont az origó. Az ilyen harmadrendû kifejezések által meghatározott görbékkel, és általában egy kétváltozós polinomot kielégítõ (x, y) pontok tulajdonságaival foglalkozik a matematika egyik legszebb, de ugyanakkor legnehezebb ága, az algebrai geometria. Elliptikus görbék a harmadrendû kifejezés által definiált nem szinguláris alakzatok. Ezek számtalan érdekes tulajdonságai közül azt használjuk fel, hogy pontjain definiálható egy mûvelet, amivel az elliptikus görbe pontjai csoportot alkotnak. Ezt a csoportot hívjuk elliptikus csoportnak. A mûveletet szokás szerint összeadásként értelmezzük, vagyis a görbe pontjait összeadhatjuk. Nullelemnek, vagyis amihez a görbe bármely más elemét adva saját magát kapjuk vissza, a formulák egyszerûsítése érdekében a görbe inflexiós pontját választjuk.
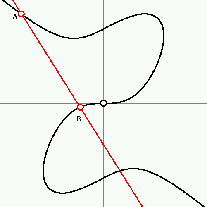
A görbe A és B pontjainak összege
Az ábrán mutatjuk be, hogyan számítjuk ki a görbe A és B pontjainak az összegét. Legyen O a görbe inflexiós pontja, ez az ábrán a koordinátarendszer középpontja. Tetszõleges egyenes a görbét egy vagy három pontban metszi, ez következik abból, hogy egy harmadfokú egyenletnek vagy egy, vagy három valós gyöke van. Ezért ha egy egyenesnek és a görbének van két közös pontja, akkor van egy harmadik is. (Speciálisan ez egybeeshet valamelyik ponttal is, ha éppen érintõrõl van szó.) Legyen tehát A és B a görbe két pontja. Kössük össze A-t és B-t egy egyenessel. Ez az egyenes a görbét még egy pontban metszi, ezt a metszéspontot kössük össze az O ponttal. Ez utóbbi egyenesnek és a görbének harmadik közös pontja lesz az A+B pont. Ha az A+A összegre vagyunk kíváncsiak, akkor természetesen az A-beli érintõt kell használni, az érintõ és a görbe metszéspontját kell O-val összekötni, és a harmadik metszéspontot választani.
Mivel az A-t és B-t összekötõ egyenes ugyanaz, mint a B-t az A-val összekötõ egyenes, azért ez a mûvelet kommutatív, vagyis A+B=B+A. Az is látszik, hogy az inflexiós pontot bármely más ponthoz hozzáadva az nem változik: A+O=O+A=A. Ez az összefüggés még az O inflexiós pontra is igaz, ugyanis az O-beli érintõ a görbét harmadszor is O-ban metszi (az O-beli érintõ harmadrendben érint). Az A ellentettjét, vagyis a (–A)-t úgy kaphatjuk meg, hogy A-t összekötjük O-val, ez az egyenes metszi ki (–A)-t a görbébõl; erre a pontra persze A+(–A)=O.
A görbénk szerencsés paraméterezése és O megválasztása miatt (–A) nem más, mint A-nak O-ra való tükörképe, ezt tehát A koordinátáiból könnyen számíthatjuk: mindkét koordinátának kell venni a (–1)-szeresét. Nem ilyen egyszerû a helyzet az (A+B) koordinátáinak számításával. Ha A az koordinátái (x1, y1), a B koordinátái pedig (x2, y2) , akkor (A+B)-nek x és y koordinátáit az alábbi, egyszerûnek semmiképpen nem mondható képletek alapján számíthatjuk (a formulákat a Maple program állította elõ):

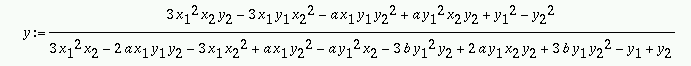
Ráadásul ezek nem használhatók abban az esetben, ha A és B egybeesik, mert ilyenkor mind a számláló mind a nevezõ nulla. Helyette másik képletet kell alkalmaznunk (azt nem mutatjuk itt be).



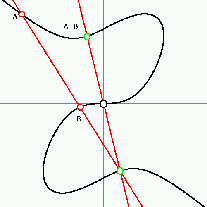
Az összeadás asszociatív: (A + B) + C = A + (B + C)
Ahhoz, hogy íly módon tényleg csoportot kapjuk, még meg kell mutatni, hogy a mûvelet asszociatív, vagyis tetszõleges A, B és C pontokra (A + B ) + C = A + (B + C). Az állítást az ábra illusztrálja. Elõször hozzáadjuk C-t az (A+B) összeghez (bal oldali ábra). Azután kiszámítjuk (B+C)-t (középsõ ábra), és ezt adjuk A-hoz. Hogy az eredmény mind a kétszer ugyanaz, következik például abból, hogy az A+B+C koordinátáit kétféleképpen kiszámítva ugyanazokat a formulákat kapjuk (nagyszerû feladat egy szimbolikus algebrai program számára). Vagy következik abból a tételbõl is, amelyet a harmadik ábráról olvashatunk le, és ami a projektív geometriából ismert Papposz tétel általánosítása. Felejtkezzünk el az A+B+C pontról és a rajta átmenõ egyenesõl. Az ábrán marad hat egyenes, melyek kilenc pontban metszik egymást. Ha e kilenc pont közül nyolc rajta van a görbén, akkor a kilencedik is rajta van. Ez a kilenc asszociált pont tétele néven ismert állítás (pontosabban annak is csak egy speciális esete).

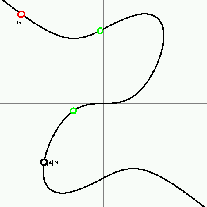

A G generáló elem és többszörösei
Ezzel megkaptuk a titkosításhoz szükséges csoportot. Amit még választanunk kell, egy G generátor (a görbe tetszõleges pontja), aminek többszöröseit használjuk fel. Szokás szerint ha G-t n-szer adjuk önmagához, az eredményt [n]G jelzi. Az ábrán láthatjuk ahogyan a G, [2]G, [3]G, stb. értékek egyre jobban beterítik a görbét. Esetünkben a diszkrét logaritmus probléma a következõ: adott a görbe paramétereivel, a G generáló pont koordinátáival, továbbá a görbének egy Q pontja. Keressük meg azt az n egész számot (ami lehet negatív is), amire Q=[n]G. Az elliptikus görbéken alapuló nyilvános kulcsú titkosírás, szokásos angol rövidítéssel ECC, éppen ennek a problémának a nehézségét használja ki.
Természetesen a gyakorlati megvalósításban a harmadfokú görbét nem a valós számok fölött használjuk, hanem valamilyen véges testet választunk erre a célra. Mivel egy véges test elemászáma mindig valamilyen prímszámhatvány, gyakorlatilag kétféle test jöhet szóba. Az egyiknél a test elemszáma egy 2n –1 alakú prímszám, a másiknál pedig kettõhatvány. A kitevõt mindkét esetben 200 körül szokás választani, így a test egy elemének felírásához ennyi bitre van szükség, a görbe egy pontját pedig két koordináta határozza meg, tehát ahhoz kétszer ennyi bitet kell tárolni.
További problémát okoz, hogy ha az alaptest elemszáma kettõhatvány, akkor az elliptikus görbe algebrai alakját nem lehet a szokásos y2 = x3 + ax + b formára hozni, hanem csak az úgynevezett Weierstrass formára: y2 + ay = x3 + bx2 + cxy + dx + e. A minél egyszerûbb alakra azért van szükség, hogy egy–egy elliptikus mûvelet végrehajtása minél gyorsabb legyen. Ahhoz, hogy két pont összegét meghatározzuk, jónéhány szorzást, összeadást, és ráadásul két osztást is el kell végeznünk az alaptest számain. Ráadásul egy kettõhatvány elemû testben két elem összege nem más, mint ezek bitenkénti mod 2 összege (vagyis a két bitsorozat XOR-ja), vagyis gyorsan számítható, addig két elem szorzatát már csak bonyolult módon (tipikusan polinomok szorzatát kell maradékosan osztani) lehet számítani. Ezért bár az ECC “csak” 200 bites számokat használ, a kódolás/dekódolás ideje nem kevesebb, mint az ötször több bitet használó RSA vagy Diffie-Hellmann módszereknek. A mûveleti igény csökkentésére több trükköt vetettek be, például a számlálót és a nevezõt külön-külön tárolják, és csak a számítás legvégén osztják el egymással. Ha a görbe egy pontjának ismerjük az x koordinátáját, akkor ehhez két lehetséges y koordináta tartozik, melyek egymás negáltjai. A számításokat el lehet úgy is végezni, hogy csak az x koordinátákkal foglalkozunk, és soha nem mondjuk meg, hogy a két lehetõség közül melyik is az igazi.
További probléma, hogy nagyon sok algoritmusban szükség van a generált csoport rendjére, vagyis arra a legkisebb r pozitív egészre, amivel [r]G = O. Ennek értékét a modulo p szorzás esetén viszonylag egyszerû megkapni, míg elliptikus görbék esetében ennek meghatározására nem ismeretes polinomiális algoritmus. A legfrisebb kutatások viszonylag gyors algoritmusokat eredményeztek, amivel egy–egy görbe rendjét már kevesebb, mint egy óra alatt meg lehet kapni.
Végül álljon itt a diszkrét logaritmus probléma egy konkrét alkalmazása. Az alábbi digitális aláírás Claus Schnorr 1991-ból származó módszerének egy változata. Elsõként az aláíró választ egy elliptikus görbét, azon egy G pontot. Meghatározza a G pont rendjét, vagyis azt a legkisebb pozitív r számot, amire [r]G = O. Választ még 0 és r–1 között egy s titkos számot, és kiszámítja a görbének a P = [s]G pontját. Az aláíró nyilvános kulcsa a következõ információkat tartalmazza: a görbét (vagyis annak a paramétereit, elõállítási módját), a G generátor pontot, valamint a P-t (illetve ennek koordinátáit).
Az M dokumentum aláírásához szükség van még egy mindenki által ismert sûrítménykészítõ algoritmusra is. Angol kifejezéssel az ilyen leképezéseket hash függvényeknek is nevezik. Léteznek minden szempontból kielégítõ tulajdonságú hash függvények, egyszerûen feltesszük hogy H( . ) egy mindenki megelégedésére kiválasztott sûrítménykészítõ eljárás, ami ráadásul mindig a generátor pont rendjénél kisebb értéket állít elõ.
Az M dokumentum aláírása a következõképpen történik. Elõször is választunk egy v véletlen számot 0 és r–1 között, majd kiszámítjuk a Q = [v]G pontot. Fûzzük hozzá a Q pont koordinátáit az M üzenethez, és számítsuk ki ennek az a = H(M, Q) sûrítményét. Most használjuk ki az aláíró s titkos értékét: meghatározzuk a v – as különbség maradékát r-rel osztva, legyen az eredmény (ami persze nem negatív, és kisebb r-nél) éppen b. Ekkor as + b ugyanakkora maradékot ad r-rel osztva, mint v, azért az elliptikus görbének az [as+b]G = [as]G + [b]G = [a]P + [b]G valamint [v]G = Q pontjai ugyanazok. Az M dokumentum aláírása az (a, b) pár.
Az aláírás hitelességének ellenõrzéséhez az M dokumentumot, annak (a, b) aláírását, és az aláíró nyilvános kulcsát használjuk. A görbe leírása, annak G valamint P pontjai ismeretében kiszámítható a görbe Q’ = [a]P + [b]G pontja. Számítsuk ki ezek után az a’ = H(M, Q’) sûrítményt. Az aláírást hitelesnek fogadjuk el, ha az így kapott a’ és az aláírásban szereplõ a szám megegyezik.
Könnyû látni, hogy egy helyesen aláírt dokumentumot mindig hitelesnek fogunk elfogadni. Ez azon múlik, hogy ilyenkor az ellenõrzéskor számított Q’ és az aláíráskor használt Q pont ugyanaz. Ahhoz, hogy az aláírást ne lehessen hamisítani, az kell, hogy a diszkrét logaritmus probléma gyakorlatilag megoldhatatlan legyen, sajnos ezen kívül még a sûrítménykészítõ H függvényrõl is különbözõ feltételeket kell tennünk. Az aláírás használatára is vannak további megszívlelendõ szabályok. Így például a v számnak nem szabad olyat választani, aminek értékét valamekkora biztonsággal meg lehet jósolni, és semmiképpen nem szabad ugyanazt a v-t különbözõ üzenetek aláírására használni.
Irodalom
[1] A. J. Menezes, P. C. van Oorschot, S. A. Vanstone: Handbook of applied cryptography, CRC Press, 1997
[2] R. Crandell, C. Pomerance: Prime numbers, a computational perspective, Springer, 2000
[3] Eric Weisstein’s world of mathematics, http://mathworld.wolfram.com
[4] N. Koblitz, Elliptic curve cryptosystems, Math.Comp, 48, 1987